Question

1. Derive the equilibrium condition for a one-person Robinson Crusoe economy and prove that the same result holds for a decentralized market economy with production and consumption sectors. Discuss the implications of the result for economic policy.

Answer 1

In the Robinson Crusoe economy, there is only one individual – Robinson Crusoe himself. He acts both as a producer to maximise profits, as well as consumer to maximise his utility. The possibility of trade can be introduced by adding another person to the economy. This person is Crusoe's friend, Man Friday. Although in the novel he plays the role of Crusoe's servant, in the Robinson Crusoe economy he is considered as another actor with equal decision making abilities as Crusoe. Along with this, conditions of Pareto Efficiency can be analysed by bringing in the concept of the Edgeworth box.

The basic assumptions of the Robinson Crusoe economy are as follows:

1. The island is cut off from the rest of the world (and hence cannot trade)
2. There is only a single economic agent (Crusoe himself)
3. All commodities on the island have to be produced or found from existing stocks

Framework

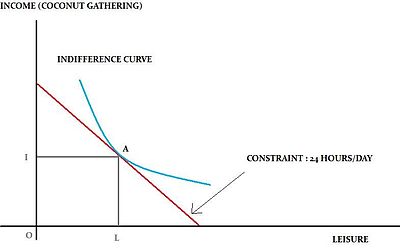
Figure: Income Leisure Preference in a Robinson Crusoe Economy.

Robinson Crusoe is assumed to be shipwrecked on a deserted island. Similar to the choices that households (suppliers of labour) face, Crusoe has only two activities to participate in – earn income or pass his time in leisure.

The income generating activity in this case is gathering coconuts. As usual, the more time he spends in leisure, the less food he has to eat, and conversely, the more time he spends gathering coconuts, the less time he has for leisure. This is depicted in figure above.

Production function and indifference curves

Crusoe's indifference curves depict his preferences for leisure and coconuts while the production function depicts the technological relationship between how much he works and how many coconuts he gathers. If the axes depicting coconut collection and leisure are reversed and plotted with Crusoe's indifference map and production function, figure 2 can be drawn:

Figure 2: The Robinson Crusoe Economy's Production Function and Indifference Curves

The production function is concave in two dimensions and quasi-convex in three dimensions. This means that the longer Robinson works, the more coconuts he will be able to gather. But due to diminishing marginal returns of labour, the additional number of coconuts he gets from every additional hour of labour is declining.

The point at which Crusoe will reach an equilibrium between the number of hours he works and relaxes can be found out when the highest indifference curve is tangent to the production function. This will be Crusoe's most preferred point provided the technology constraint is given and cannot be changed. At this equilibrium point, the slope of the highest indifference curve must equal the slope of the production function.

Recall that the Marginal rate of substitution is the rate at which a consumer is ready to give up one good in exchange for another good while maintaining the same level of utility. Additionally, an input's marginal product is the extra output that can be produced by using one more unit of the input, assuming that the quantities of no other inputs to production change. Then,

MP_L = MRS_{Leisure, Coconuts}

where,

MP_L = Marginal Product of Labour, and

MRS_{Leisure, Coconuts} = Marginal rate of substitution between Leisure and Coconuts

Crusoe's multifaceted role

Suppose Crusoe decides to stop being a producer and consumer simultaneously. He decides he will produce one day and consume the next. His two roles of consumer and producer are being split up and studied separately to understand the elementary form of consumer theory and producer theory in microeconomics. For dividing his time between being a consumer and producer, he must set up two collectively exhaustive markets, the coconut market and the labour market. He also sets up a firm, of which he becomes the sole shareholder. The firm will want to maximise profits by deciding how much labour to hire and how many coconuts to produce according to their prices. As a worker of the firm, Crusoe will collect wages, as a shareholder, he will collect profits and as a consumer, he will decide how much of the firm's output to purchase according to his income and the prevailing market prices. Let's assume that a currency called "Dollars" has been created by Robinson to manage his finances. For simplicity, assume that Price_Coconuts = $1.00. This assumption is made to make the calculations in the numerical example easy because the inclusion of prices will not alter the result of the analysis. For more details, refer to Numéraire commodities.

Producer

Figure 3: Profit Maximising Condition for the firm in the Robinson Crusoe Economy

Assume that when the firm produces C amount of total coconuts, represents its profit level. Also assume that when the wage rate at which the firm employs labour is w, L amount of labour will be employed. Then,

The above function describes iso-profit lines (the locus of combinations between labour and coconuts that produce a constant profit of ?). Profits can be maximised when the marginal product of labour equals the wage rate (marginal cost of production). Symbolically,

MP_L = w

Graphically, the iso-profit line must be tangent to the production function.

The vertical intercept of the iso-profit line measures the level of profit that Robinson Crusoe's firm will make. This level of profit, ?, has the ability to purchase ? dollars worth of coconuts. Since Price_Coconuts is $1.00, ? number of coconuts can be purchased. Also, the firm will declare a dividend of ? dollars. This will be given to the firm's sole shareholder, Crusoe himself.

Consumer

Figure 4: Robinson Crusoe's Maximisation Problem showing his budget line and indifference curve

As a consumer, Crusoe will have to decide how much to work (or indulge in leisure) and hence consume. He can choose to not work at all, since he has an endowment of ? dollars from being a shareholder. Let us instead consider the more realistic case of him deciding to work for a few hours. His labour consumption choice can be illustrated in figure 4:

Note that labour is assumed to be a 'bad', i.e., a commodity that a consumer doesn't like. Its presence in his consumption basket lowers the utility he derives.^[1] On the other hand, coconuts are goods. This is why the indifference curves are positively sloped. The maximum amount of labour is indicated by L'. The distance from L' to the chosen supply of labour (L*) gives Crusoe's demand for leisure.

Notice Crusoe's budget line. It has a slope of w and passes through the point (0,?). This point is his endowment level i.e., even when he supplies 0 amount of labour, he has ? amount of coconuts (dollars) to consume. Given the wage rate, Crusoe will choose how much to work and how much to consume at that point where,

MRS_{Leisure, Coconuts} = w

Equilibrium

Figure 5: Equilibrium in both production and consumption in the Robinson Crusoe Economy

At equilibrium, the demand for coconuts will equal the supply of coconuts and the demand for labour will equal the supply of labour.^[4]

Graphically this occurs when the diagrams under consumer and producer are superimposed.^[7]Notice that,

MRS_{Leisure, Coconuts} = w

MP_L = w

-=> MRS_{Leisure, Coconuts} = MP_L

This ensures that the slopes of the indifference curves and the production set are the same.

As a result, Crusoe ends up consuming at the same point he would have if he made all the above decisions together. In other words, using the market system has the same outcome as choosing the individual utility maximisation and cost minimisation plans. This is an important result when put into a macro level perspective because it implies that there exists a set of prices for inputs and outputs in the economy such that the profit-maximising behaviour of firms along with the utility-maximizing actions of individuals results in the demand for each good equaling the supply in all markets. This means that a competitive equilibrium can exist. The merit of a competitive equilibrium is that an efficient allocation of resources is achievable.^[1] In other words, no economic agent can be made better off without making another economic agent worse off.^[8]

Production possibilities with two goods

Let's assume that there is another commodity that Crusoe can produce apart from coconuts, for example, fish. Now, Robinson has to decide how much time to spare for both activities, i.e. how many coconuts to gather and how many fish to hunt. The locus of the various combinations of fish and coconuts that he can produce from devoting different amounts of time to each activity is known as the production possibilities set. This is depicted in the figure 6:

Figure 6: Production possibilities set in the Robinson Crusoe economy with two commodities.

The boundary of the production possibilities set is known as the Production-possibility frontier (PPF). This curve measures the feasible outputs that Crusoe can produce, with a fixed technological constraint and given amount of resources. In this case, the resources and technological constraints are Robinson Crusoe's labour.

It is crucial to note that the shape of the PPF depends on the nature of the technology in use. Here, technology refers to the type of returns to scale prevalent. In figure 6, the underlying assumption is the usual decreasing returns to scale, due to which the PPF is concave to the origin. In case we assumed increasing returns to scale, say if Crusoe embarked upon a mass production movement and hence faced decreasing costs, the PPF would be convex to the origin. The PPF is linear with a downward slope in two circumstances:

1. If the technology for gathering coconuts and hunting fish exhibits constant returns to scale
2. If there is only one input in production

So in the Robinson Crusoe economy, the PPF will be linear due to the presence of only one input.

Marginal rate of transformation

Suppose that Crusoe can produce 4 pounds of fish or 8 pounds of coconuts per hour. If he devotes L_f hours to fish gathering and L_c hours to gathering coconuts, he will produce 4L_f pounds of fish and 8L_c pounds of coconuts. Suppose that he decides to work for 12 hours a day. Then the production possibilities set will consist of all combinations of fish, F, and coconuts, C, such that

Solve the first two equations and substitute in the third to get,

This equation represents Crusoe's PPF. The slope of this PPF measures the Marginal rate of transformation (MRT), i.e., how much of the first good must be given up in order to increase the production of the second good by one unit. If Crusoe works one hour less on hunting fish, he will have 4 less fish. If he devotes this extra hour to collecting coconuts, he will have 8 extra coconuts. The MRT is thus,

MRT _{Coconuts, Fish}

Comparative advantage

Under this section, the possibility of trade is introduced by adding another person to the economy. Suppose that the new worker who is added to the Robinson Crusoe Economy has different skills in gathering coconuts and hunting fish. The second person is called "Friday".

Friday can produce 8 pounds of fish or 4 pounds of coconuts per hour. If he too decides to work for 12 hours, his production possibilities set will be determined by the following relations:

Thus, MRT _{Coconuts, Fish}

This means that for every pound of coconuts Friday gives up, he can produce 2 more pounds of fish.

So, we can say that Friday has a Comparative advantage  in hunting fish while Crusoe has a comparative advantage in gathering coconuts. Their respective PPFs can be shown in the following diagram:

Figure 7: Joint production possibilities in the Robinson Crusoe economy.

The joint production possibilities set at the extreme right shows the total amount of both commodities that can be produced by Crusoe and Friday together. It combines the best of both workers. If both of them work to gather coconuts only, the economy will have 144 coconuts in all, 96 from Crusoe and 48 from Friday. (This can be obtained by setting F=0 in their respective PPF equations and summing them up). Here the slope of the joint PPF is -1/2.

If we want more fish, we should shift that person who has a comparative advantage in fish hunting (i.e. Friday) out of coconut gathering and into fish hunting. When Friday is producing 96 pounds of fish, he is fully occupied. If fish production is to be increased beyond this point, Crusoe will have to start hunting fish. Here onward, the slope of the joint PPF is -2. If we want to produce only fish, then the economy will have 144 pounds of fish, 48 from Crusoe and 96 from Friday. Thus the joint PPF is kinked because Crusoe and Friday have comparative advantages in different commodities. As the economy gets more and more ways of producing output and different comparative advantages, the PPF becomes concave.^[1]

Pareto efficiency

Assume that there are c units of coconut and f units of fish available for consumption in the Crusoe Friday economy. Given this endowment bundle (c,f), the Pareto efficient bundle can be determined at the mutual tangency of Crusoe's and Friday's indifference curves in the Edgeworth box along the Pareto Set (Contract curve). These are the bundles at which Crusoe's and Friday's Marginal rate of substitution are equal. In a simple exchange economy, the contract curve describes the set of bundles that exhaust the gains from trade. But in a Robinson Crusoe/Friday economy, there is another way to exchange goods – to produce less of one good and more of the other.

Figure 8: Production Possibilities Set in Robinson Crusoe Economy and the Edgeworth Box showing a Pareto Efficient situation within

From the figure 8, it is clear that an economy operating at a position where the MRS of either Crusoe or Friday is not equal to the MRT between coconuts and fish cannot be Pareto efficient. This is because the rate at which, say Friday is willing to trade coconuts for fish is different from the rate at which coconuts can be transformed into fish. Thus, there is a way to make Friday better off by rearranging the production pattern.

Thus for Pareto Efficiency,

MRT _{Coconuts, Fish} = MRS_{Coconuts, Fish} ^[9]

(for both Crusoe and Friday)

This can be achieved in a competitive market by decentralising production and consumption decisions, i.e. Crusoe and Friday will both solve their own problems of how much to consume and produce independently.