Question

In: Statistics and Probability

3. Workers at an orchard recorded the weights of 1000 avocados. The weights are approximately normally...

3. Workers at an orchard recorded the weights of 1000 avocados. The weights are approximately normally distributed, with a mean weight of 225 grams and a standard deviation of 25 grams. Which of the following statements are true? Select all that apply.

A. Approximately 34% of the avocados weight between 225 and 250 grams. B. Approximately 50% of the avocados weigh 225 grams.

C. Approximately 500 of the avocados weigh more than 200 grams.

D. Approximately 160 avocados weigh more than 250 grams.

E. Approximately 84% of the avocados weigh less than 250 grams.

Expert Solution

Let X denotes the weight of a randomly selected worker.

X ~ Normal(225, 25²)

A)

So, Approximately 34% of the avocados weight between 225 and 250 grams.

B)

So, Approximately 50% of the avocados weigh 225 grams.

C)

Number of avocados weigh more than 200 grams = 1000*0.8413 = 841.3

D)

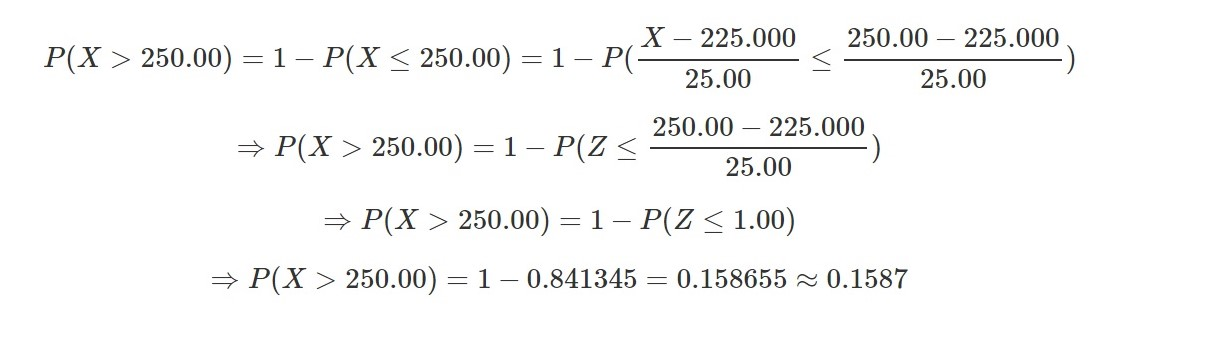
Number of avocados weigh more than 250 grams = 100*0.1587 = 158.7 160

E)

Approximately 84% of the avocados weigh less than 250 grams.

Hence,

The TRUE statements are -

A. Approximately 34% of the avocados weight between 225 and 250 grams.

B. Approximately 50% of the avocados weigh 225 grams.

D. Approximately 160 avocados weigh more than 250 grams.

E. Approximately 84% of the avocados weigh less than 250 grams.

orchestra answered 2 years ago

1. A new breed of avocados has weights that are normally distributed with mean of µ...

1. A new breed of avocados has weights that are normally distributed with mean of µ = 110 grams and population standard deviation σ = 16 grams. (a) What is the probability that any one randomly chosen avocado would have a weight of 120 grams or above? Shade the appropriate region in the normal distribution plot. Be sure to plot and label the observed weight on the horizontal axis. Also label the center of the distribution with the appropriate value....

The weights of healthy domesticated kittens at ten weeks of age are approximately are approximately normally...

The weights of healthy domesticated kittens at ten weeks of age are approximately are approximately normally distributed with a mean of 23 ounces and a standard deviation of 3.7 ounces. Approximately 68% of kittens weigh between (, ) ounces. Approximately 95% of kittens weigh between (, ) ounces. Approximately 99.7% of kittens weigh between (, ) ounces. The heights of women have a symmetric distribution with a mean of 66 inches and a standard deviation of 2.5 inches. Approximately 68%...

The weights for newborn babies is approximately normally distributed with a mean of 5lbs and a...

The weights for newborn babies is approximately normally distributed with a mean of 5lbs and a standard deviation of 1.5lbs. Consider a group of 1,000 newborn babies: How many would you expect to weigh between 4-7lbs? How many would you expect to weigh less than 6lbs? How many would you expect to weigh more than 5lbs? How many would you expect to weigh between 5-10lbs?

The weights of a large number of miniature poodles are approximately normally distributed with a man...

The weights of a large number of miniature poodles are approximately normally distributed with a man of 8 kilograms and a standard deviation of 0.9 kilograms. Find the fraction of these poodles with weight over 9.55 kilograms.

The weights for newborn babies is approximately normally distributed with a mean of 6.9 pounds and...

The weights for newborn babies is approximately normally distributed with a mean of 6.9 pounds and a standard deviation of 1.1 pounds. Consider a group of 1200 newborn babies: 1. How many would you expect to weigh between 6 and 9 pounds? 2. How many would you expect to weigh less than 8 pounds? 3. How many would you expect to weigh more than 7 pounds? 4. How many would you expect to weigh between 6.9 and 10 pounds?

The weights of a certain dog breed are approximately normally distributed with a mean of 50...

The weights of a certain dog breed are approximately normally distributed with a mean of 50 pounds, and a standard deviation of 6 pounds. Use your graphing calculator to answer the following questions. Write your answers in percent form. Round your answers to the nearest tenth of a percent. a) Find the percentage of dogs of this breed that weigh less than 50 pounds. % b) Find the percentage of dogs of this breed that weigh less than 48 pounds....

The weights of a certain dog breed are approximately normally distributed with a mean of μμ...

The weights of a certain dog breed are approximately normally distributed with a mean of μμ = 56 pounds, and a standard deviation of σσ = 7 pounds. A dog of this breed weighs 45 pounds. What is the dog's z-score? Round your answer to the nearest hundredth as needed. z= A dog has a z-score of -0.53. What is the dog's weight? Round your answer to the nearest tenth as needed. ……… pounds A dog has a z-score of...

The weights of a certain dog breed are approximately normally distributed with a mean of 49...

The weights of a certain dog breed are approximately normally distributed with a mean of 49 pounds, and a standard deviation of 6.3 pounds. Answer the following questions. Write your answers in percent form. Round your answers to the nearest tenth of a percent. a) Find the percentage of dogs of this breed that weigh less than 49 pounds. % b) Find the percentage of dogs of this breed that weigh less than 46 pounds. % c) Find the percentage...

A population of women’s weights is approximately normally distributed with a mean of 140 lb and...

A population of women’s weights is approximately normally distributed with a mean of 140 lb and a standard deviation of 20 lb. What percentage of women weigh between 120 and 160 lb? If samples of size 16 are drawn from the population of women’s weights, what percentage of the sample means lie between 120 and 160 lb? What is the probability that a sample mean from a sample size 16 lies above 145 lb?

The weights of a certain dog breed are approximately normally distributed with a mean of 52...

The weights of a certain dog breed are approximately normally distributed with a mean of 52 pounds, and a standard deviation of 6.7 pounds. Answer the following questions. Write your answers in percent form. Round your answers to the nearest tenth of a percent. a) Find the percentage of dogs of this breed that weigh less than 52 pounds. b) Find the percentage of dogs of this breed that weigh less than 47 pounds. c) Find the percentage of dogs...