Question
In: Math
It is estimated that approximately 8.17% Americans are afflicted with diabetes. Suppose that a certain diagnostic...
It is estimated that approximately 8.17% Americans are afflicted with diabetes. Suppose that a certain diagnostic evaluation for diabetes will correctly diagnose 98% of all adults over 40 with diabetes as having the disease and incorrectly diagnoses 3% of all adults over 40 without diabetes as having the disease. a) Find the probability that a randomly selected adult over 40 does not have diabetes, and is diagnosed as having diabetes (such diagnoses are called "false positives"). b) Find the probability that a randomly selected adult of 40 is diagnosed as not having diabetes. c) Find the probability that a randomly selected adult over 40 actually has diabetes, given that he/she is diagnosed as not having diabetes (such diagnoses are called "false negatives"). (Note: it will be helpful to first draw an appropriate tree diagram modeling the situation)
Solutions
Expert Solution
Solution:
Let
TP = Test Positive
TN = Test Negative
D = having diabetes
ND = Not having diabetes
Thus we have:
8.17% Americans are afflicted with diabetes.
That is:
P(D) = 0.0817
P(ND) = 1 - P(D)
P(ND) = 1 - 0.0817
P(ND) = 0.9183
A certain diagnostic evaluation for diabetes will correctly diagnose 98% of all adults over 40 with diabetes as having the disease
P( TP | D) = 0.98
and
incorrectly diagnoses 3% of all adults over 40 without diabetes as having the disease
P( TP | ND)= 0.03
Thus Tree diagram is:
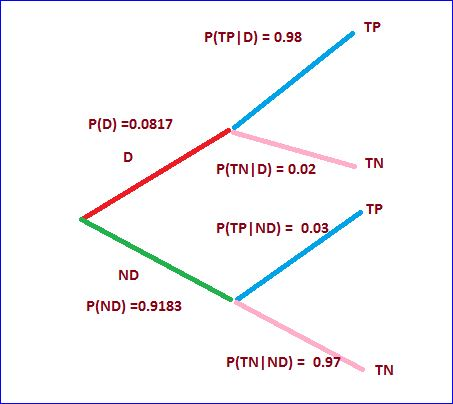
Part a) Find the probability that a randomly selected adult over 40 does not have diabetes, and is diagnosed as having diabetes
P( Does not have diabetes, and is diagnosed as having diabetes) = ........?
P( ND and TP ) =............?
Using: P( TP | ND)= 0.03 and conditional probability formula:
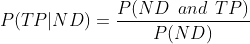
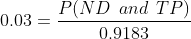

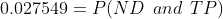

Part b) Find the probability that a randomly selected adult of 40 is diagnosed as not having diabetes.
That is find:
P( TN) = ..........?
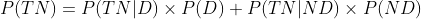
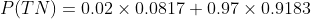
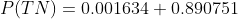

Part c) Find the probability that a randomly selected adult over 40 actually has diabetes, given that he/she is diagnosed as not having diabetes
P(D | TN) =.............?
Using Bayes rule:
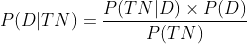
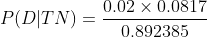
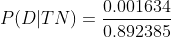
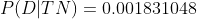
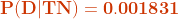
Related Solutions
(1 point) It is estimated that approximately 8.1% of Americans are afflicted with diabetes. Suppose that...
Suppose the lengths of the pregnancies of a certain animal are approximately distributed with a mean...
A certain medical test is known to detect 72% of the people who are afflicted with...
A certain medical test is known to detect 73% of the people who are afflicted with...
A certain medical test is known to detect 50% of the people who are afflicted with...
A certain medical test is known to detect 49% of the people who are afflicted with...
A certain medical test is known to detect 38% of the people who are afflicted with...
Suppose the lengths of the pregnancies of a certain animal are approximately normally distributed with mean...
Suppose the lengths of the pregnancies of a certain animal are approximately normally distributed with mean...
Suppose the lengths of the pregnancies of a certain animal are approximately normally distributed with mean...
- Write a program that manages a list of patients for a medical office. Patients should be...
- 1- Activity-Based Costing: Explain three (3) reasons in details, why all manufacturing companies don’t use an...
- If you take a two-litre plastic soda bottle and blow across the lid, you get a...
- A positron with kinetic energy 2.5 keV is projected into a uniform magnetic field Bvec of...
- examples of where a country/Today/ has an Absolute Advantage, and why there is an increase in...
- Suppose the charge q2 in the figure can be moved left or right along the line...
- define the following functional plans MBO mission
 milcah answered 1 year ago
milcah answered 1 year ago