Question
In: Math
Water specimens are taken from water used for cooling as it is being discharged from a...
Water specimens are taken from water used for cooling as it is being discharged from a power plant into a river. It has been determined that as long as the mean temperature of the discharged water is at most 150°F, there will be no negative effects on the river's ecosystem. To investigate whether the plant is in compliance with regulations that prohibit a mean discharge water temperature above 150°F, researchers will take 50 water specimens at randomly selected times and record the temperature of each specimen. The resulting data will be used to test the hypotheses
H0: μ = 150°F
versus
Ha: μ > 150°F.
(a) In the context of this example, describe Type I and Type II errors. (Select all that apply.)
A Type I error is not obtaining convincing evidence that the mean water temperature is greater than 150°F when in fact it is greater than 150°F.
A Type I error is obtaining convincing evidence that the mean water temperature is greater than 150°F when in fact it is (at most) 150°F.
A Type II error is obtaining convincing evidence that the mean water temperature is greater than 150°F when in fact it is (at most) 150°F.
A Type II error is not obtaining convincing evidence that the mean water temperature is greater than 150°F when in fact it is greater than 150°F.
A magazine collects data each year on the price of a hamburger in a certain fast food restaurant in various countries around the world. The price of this hamburger for a sample of restaurants in Europe in January resulted in the following hamburger prices (after conversion to U.S. dollars).
| 5.17 | 4.93 | 4.09 | 4.67 | 5.22 | 4.69 |
| 4.15 | 4.97 | 5.13 | 5.53 | 5.36 | 4.60 |
The mean price of this hamburger in the U.S. in January was $4.61. For purposes of this exercise, assume it is reasonable to regard the sample as representative of these European restaurants. Does the sample provide convincing evidence that the mean January price of this hamburger in Europe is greater than the reported U.S. price? Test the relevant hypotheses using
α = 0.05.
(Use a statistical computer package to calculate the P-value. Round your test statistic to two decimal places and your P-value to three decimal places.)
| t | = | |
| P-value | = |
Medical research has shown that repeated wrist extension beyond 20 degrees increases the risk of wrist and hand injuries. Each of 24 students at a university used a proposed new computer mouse design. While using the mouse, each student's wrist extension was recorded. Data consistent with summary values given in a paper are given. Use these data to test the hypothesis that the mean wrist extension for people using this new mouse design is greater than 20 degrees. (Use
α = 0.05.
Use a statistical computer package to calculate the P-value. Round your test statistic to two decimal places and your P-value to three decimal places.)
| 26 | 28 | 25 | 27 | 26 | 24 | 24 | 25 | 25 | 25 | 24 | 28 |
| 22 | 24 | 25 | 28 | 26 | 27 | 31 | 24 | 28 | 26 | 26 | 24 |
| t | = | |
| P-value | = |
Solutions
Expert Solution

Explanation : Type I error is probability of rejecting null when it is actually true. Type II error is accepting null when it is actually False. Above answers are obtained from this definitions.
2.
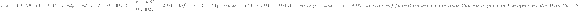
3
.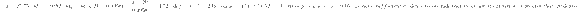
Related Solutions
1.Water samples were taken from water used for cooling as it was being discharged from a...
Contaminated water: In a sample of 42 water specimens taken from a construction site, 26 contained...
In a sample of 59 water specimens taken from a construction site, 22 contained detectable levels...
A wet cooling tower is to cool 25 kg/sec of cooling water from 40oC to 25oC...
It is noteworthy that during a holiday trip, the water is discharged from a high tank...
Thirty-two 1-Liter specimens of water were drawn from the water supply for a city and the...
In California treated wastewater is normally disinfected before being discharged to natural water bodies. Briefly state...
A water tower is being used to provide water to a subdivision. To ensure that it...
Organisms are present in ballast water discharged from a ship according to a Poisson process with...
Organisms are present in ballast water discharged from a ship according to a Poisson process with...
- C++ langugae only The first phase of compilation is called scanning or lexical analysis. This phase...
- 3. Mechanism of carbocation Rearrangements (hydride shift and methyl shift). Can you please explain what you...
- The unemployments number of US for 2019 is 3.7%, and for the year 2010 is 9.7%...
- 1. some people are sensitive to aspirin. Why ? 2. relate excess aspirin inrake to a...
- Difference between Granovetter’s view of economic and Adam smith economic behavior theory?
- three autosomal genes (Z, E and T) in seahorses. Each gene sorts independently and each gene...
- Q1. What additional concerns might a corporate Chief Financial Officer (CFO) face when a company expands...
 milcah answered 1 year ago
milcah answered 1 year ago