Let A = {1, 2, 3, 4, 5}. Find the inverse of the following functions f:...

Let A = {1, 2, 3, 4, 5}. Find the inverse of the following functions f: A→ A.

1. ? = {(1,1),(2,3),(3,2),(4,4),(5,5)
1. ? = {(1,5),(2,4),(3,2),(4,1),(5, 4)}
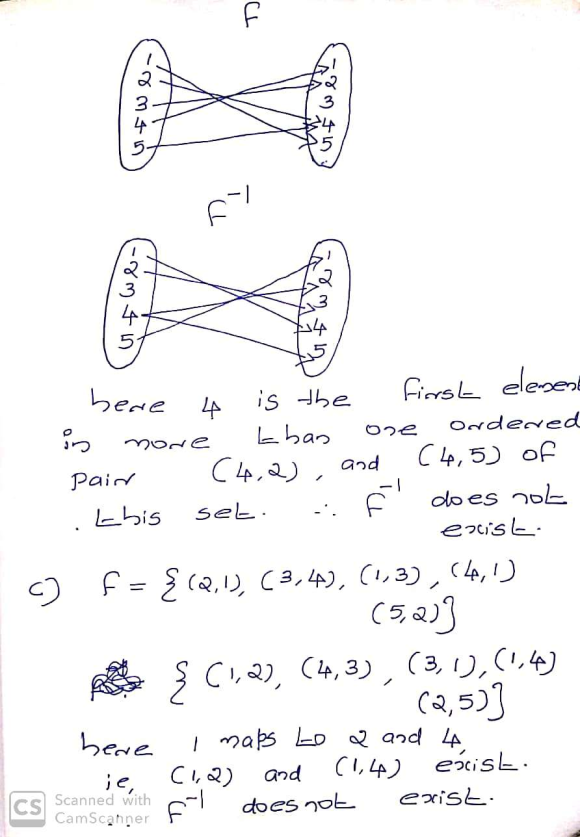
1. ? = {(2,1),(3,4),(1,3),(4,1),(5, 2)}

Expert Solution

in a function that associates to every element of the first set exactly one element in the second set.if (x,y) is in f then (y,x) is in f^-1.

In (b) when we consider the ordered pairs of f^-1, the element 4 maps to both 2 and 5,so f^-1 is not a function.so f^-1 does not exist.

In (c) f^-1 has a ordered pairs (1,2) and (1,4) so it is not a function .so f^-1 does not exist.

Inverse function is a function by definition.

Colby Messinger answered 1 day ago

3. Let X = {1, 2, 3, 4}. Let F be the set of all functions...

3. Let X = {1, 2, 3, 4}. Let F be the set of all functions from X to X. For any relation R on X, define a relation S on F by: for all f, g ∈ F, f S g if and only if there exists x ∈ X so that f(x)Rg(x). For each of the following statements, prove or disprove the statement. (a) For all relations R on X, if R is reflexive then S is reflexive....

2. Consider functions f : {1, 2, 3, 4, 5, 6} → {1, 2, 3, 4,...

2. Consider functions f : {1, 2, 3, 4, 5, 6} → {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. (a) How many of these functions are strictly increasing (i.e. f(1) < f(2) < f(3) < f(4) < f(5) < f(6))? Hint: How many different possibilities are there for the range of f? For each range of f, how many strictly increasing functions are there? (b) How many of these functions are non-decreasing (i.e. f(1) ≤ f(2) ≤...

Find the inverse of the matrix [ 1 1 4 ] [ 3 2 4 ]...

Find the inverse of the matrix [ 1 1 4 ] [ 3 2 4 ] [ 1 1 6 ] It is a 3*3 matrix

6. Let A = {1, 2, 3, 4} and B = {5, 6, 7}. Let f...

6. Let A = {1, 2, 3, 4} and B = {5, 6, 7}. Let f = {(1, 5),(2, 5),(3, 6),(x, y)} where x ∈ A and y ∈ B are to be determined by you. (a) In how many ways can you pick x ∈ A and y ∈ B such that f is not a function? (b) In how many ways can you pick x ∈ A and y ∈ B such that f : A → B...

let A =[4 -5 2 -3] find eigenvalues of A find eigenvector of A corresponding to...

let A =[4 -5 2 -3] find eigenvalues of A find eigenvector of A corresponding to eigenvlue in part 1 find matrix D and P such A= PDP^-1 compute A^6

Let f (x) = 12x^5 + 15x^4 − 40x^3 + 1, defined on R. (a) Find...

Let f (x) = 12x^5 + 15x^4 − 40x^3 + 1, defined on R. (a) Find the intervals where f is increasing, and decreasing. (b) Find the intervals where f is concave up, and concave down. (c) Find the local maxima, the local minima, and the inflection points. (d) Find the Maximum and Minimum Absolute of f over [−2, 2].

part 1) Let f(x) = x^4 − 2x^2 + 3. Find the intervals of concavity of...

part 1) Let f(x) = x^4 − 2x^2 + 3. Find the intervals of concavity of f and determine its inflection point(s). part 2) Find the absolute extrema of f(x) = x^4 + 4x^3 − 8x^2 + 3 on [−1, 2].

4) Let ? = {2, 3, 5, 7}, ? = {3, 5, 7}, ? = {1,...

4) Let ? = {2, 3, 5, 7}, ? = {3, 5, 7}, ? = {1, 7}. Answer the following questions, giving reasons for your answers. a) Is ? ⊆ ?? b)Is ? ⊆ ?? c) Is ? ⊂ ?? d) Is ? ⊆ ?? e) Is ? ⊆ ?? 5) Let ? = {1, 3, 4} and ? = {2, 3, 6}. Use set-roster notation to write each of the following sets, and indicate the number of elements in...

a) Let σ = (1 2 3 4 5 6) ∈ S6, find the cycle decomposition...

a) Let σ = (1 2 3 4 5 6) ∈ S6, find the cycle decomposition of σ i for i = 1, 2, . . . , 6. (b) Let σ1, . . . , σm ∈ Sn be disjoint cycles. For 1 ≤ i ≤ m, let ki be the length of σi . Determine o(σ1σ2 · · · σm)

Let X = {1, 2, 3, 4, 5, 6} and let ∼ be given by {(1,...

Let X = {1, 2, 3, 4, 5, 6} and let ∼ be given by {(1, 1),(2, 2),(3, 3),(4, 4),(5, 5),(6, 6),(1, 3),(1, 5),(2, 4),(3, 1),(3, 5), (4, 2),(5, 1),(5, 3)}. Is ∼ an equivalence relation? If yes, write down X/ ∼ .

Question