Question

Research and summarize the concept of the Qauntum Computer and explain the concept of the Qubit as opposed to the traditional bit. Assess the viability of actually building one of these contraptions and identify some of the main physical/engineering barriers that exist to actually building one of these devices.

Answer 1

A quantum computer with a given number of qubits is fundamentally different from a classical computer composed of the same number of classical bits. For example, to represent the state of an n-qubit system on a classical computer would require the storage of 2ⁿcomplex coefficients. Although this fact may seem to indicate that qubits can hold exponentially more information than their classical counterparts, care must be taken not to overlook the fact that the qubits are only in a probabilistic superposition of all of their states. This means that when the final state of the qubits is measured, they will only be found in one of the possible configurations they were in before measurement. Moreover, it is incorrect to think of the qubits as only being in one particular state before measurement since the fact that they were in a superposition of states before the measurement was made directly affects the possible outcomes of the computation.

Qubits are made up of controlled particles and the means of control (e.g. devices that trap particles and switch them from one state to another).^[10]

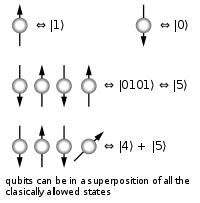
For example: Consider first a classical computer that operates on a three-bit register. The state of the computer at any time is a probability distribution over the 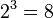different three-bit strings 000, 001, 010, 011, 100, 101, 110, 111. If it is a deterministic computer, then it is in exactly one of these states with probability 1. However, if it is a probabilistic computer, then there is a possibility of it being in any one of a number of different states. We can describe this probabilistic state by eight nonnegative numbers A,B,C,D,E,F,G,H (where A = probability computer is in state 000, B = probability computer is in state 001, etc.). There is a restriction that these probabilities sum to 1.

The state of a three-qubit quantum computer is similarly described by an eight-dimensional vector (a,b,c,d,e,f,g,h), called a ket. Here, however, the coefficients can have complex values, and it is the sum of the squares of the coefficients' magnitudes, , that must equal 1. These square magnitudes represent the probability amplitudes of given states. However, because a complex number encodes not just a magnitude but also a direction in the complex plane, the phase difference between any two coefficients (states) represents a meaningful parameter. This is a fundamental difference between quantum computing and probabilistic classical computing.^[11]

If you measure the three qubits, you will observe a three-bit string. The probability of measuring a given string is the squared magnitude of that string's coefficient (i.e., the probability of measuring 000 = 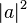, the probability of measuring 001 = , etc..). Thus, measuring a quantum state described by complex coefficients (a,b,...,h) gives the classical probability distribution and we say that the quantum state "collapses" to a classical state as a result of making the measurement.

Note that an eight-dimensional vector can be specified in many different ways depending on what basis is chosen for the space. The basis of bit strings (e.g., 000, 001, ..., 111) is known as the computational basis. Other possible bases are unit-length, orthogonal vectors and the eigenvectors of the Pauli-x operator. Ket notation is often used to make the choice of basis explicit. For example, the state (a,b,c,d,e,f,g,h) in the computational basis can be written as:

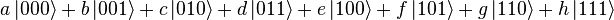
where, e.g.,

The computational basis for a single qubit (two dimensions) is and .

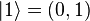Using the eigenvectors of the Pauli-x operator, a single qubit is and .