Question

In: Physics

In terms of λ, f, μ, and T what times the square root of the tension...

In terms of λ, f, μ, and T what times the square root of the tension is equal to the wavelength?

Please show work, thanks.

Expert Solution

The speed of propagation of a wave in a string () is proportional to the square root of the tension of the string () and inversely proportional to the square root of the linear density () of the string:

Derivation:

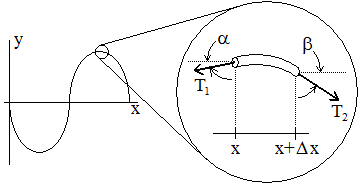
Let 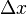be the length of a piece of string, its mass, and its linear density. If the horizontal component of tension in the string is a constant, , then the tension acting on each side of the string segment is given by

If both angles are small, then the tensions on either side are equal and the net horizontal force is zero. From Newton's second law for the vertical component, the mass of this piece times its acceleration, , will be equal to the net force on the piece:

Dividing this expression by and substituting the first and second equations obtains

The tangents of the angles at the ends of the string piece are equal to the slopes at the ends, with an additional minus sign due to the definition of beta. Using this fact and rearranging provides

In the limit that 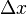approaches zero, the left hand side is the definition of the second derivative of :

This is the wave equation for , and the coefficient of the second time derivative term is equal to ; thus

where is the speed of propagation of the wave in the string. (See the article on the wave equation for more about this). However, this derivation is only valid for vibrations of small amplitude; for those of large amplitude, 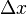is not a good approximation for the length of the string piece, the horizontal component of tension is not necessarily constant, and the horizontal tensions are not well approximated by .

Once the speed of propagation is known, the frequency of the sound produced by the string can be calculated. The speed of propagation of a wave is equal to the wavelength divided by the period , or multiplied by the frequency :

If the length of the string is , the fundamental harmonic is the one produced by the vibration whose nodes are the two ends of the string, so is half of the wavelength of the fundamental harmonic. Hence one obtains Mersenne's laws:

where is the tension (in Newton), is the linear density (that is, the mass per unit length), and is the length of the vibrating part of the string.

lambda=(1/f) sqrt (T/mu)

This is the required derivation.

genius_generous answered 1 year ago

Estimate the area A between the graph of the function f(x)= square root of x and...

Estimate the area A between the graph of the function f(x)= square root of x and the interval [0,49]. Use an approximation scheme with n=2,5, and 10 rectangles. Use the right endpoints. Round your answers to three decimal places. A2= A5= A10= Click

What is the concept of the square root of time rule?

What is the root-sum-square uncertainty model?

Let X ~ exp(λ) MGF of X = λ/(1-t) a) What is MGF of Y =...

Let X ~ exp(λ) MGF of X = λ/(1-t) a) What is MGF of Y = 3X b) Y has a common distribution, what is the pdf of Y? c) Let X1,X2,....Xk be independent and identically distributed with Xi ~ exp(λ) and S = Σ Xi (with i = 1 below the summation symbol, and k is on top of the summation symbol). What is the MGF of S? d) S has a common distribution. What is the pdf of...

Use f(x) = ?2x, g(x) = square root of x and h(x) = |x| to find...

Use f(x) = ?2x, g(x) = square root of x and h(x) = |x| to find and simplify expressions for the following functions and state the domain of each using interval notation. a . (h ? g ? f)(x) b. (h ? f ? g)(x) (g ? f ? h)(x)

Let T∈ L(V), and let p ∈ P(F) be a polynomial. Show that if p(λ) is...

Let T∈ L(V), and let p ∈ P(F) be a polynomial. Show that if p(λ) is an eigenvalue of p(T), then λ is an eigenvalue of T. Under the additional assumption that V is a complex vector space, and conclude that {μ | λ an eigenvalue of p(T)} = {p(λ) | λan eigenvalue of T}.

Differentiate the following: 1) f(x) = √2x-4. (all under square root) 2) f(x) = x/5-x 3)...

Differentiate the following: 1) f(x) = √2x-4. (all under square root) 2) f(x) = x/5-x 3) y=cos(4x^3) 4) f(x)=tan(x^2) 5) f(x)= 3e^2x cos(2x) 6) y= sin2x/cosx 7) y= √sin(cosx) (all under the square root)

Let X and Y have joint PDF f(x) = c(e^-(x/λ + y/μ)) 0 < x <...

Let X and Y have joint PDF f(x) = c(e^-(x/λ + y/μ)) 0 < x < infinity and 0 < y < infinity with parameters λ > 0 and μ > 0 a) Find c such that this is a PDF. b) Show that X and Y are Independent c) What is P(1 < X < 2, 0 < Y < 5) ? Leave in exponential form d) Find the marginal distribution of Y, f(y) e) Find E(Y)

3.Both F and Chi Square distributions can be used to compare multiple sample means T/F 4.For...

3.Both F and Chi Square distributions can be used to compare multiple sample means T/F 4.For Chi Square tests, all tests discussed can be used for both experiments and surveys T/F

T or F: The stock market far exceeds the bond market in terms of size of...

T or F: The stock market far exceeds the bond market in terms of size of new capital raised. T or F: The NASDAQ Market is composed of large nationwide companies that are traded in the over-the-counter market. When global capital markets collectively react to international events, like Russia's default on its sovereign debt, it is common to find A.that there is no impact on the trade of foreign goods. B.an impact on the ability to raise capital. C.that Wall...