Question
In: Electrical Engineering
create simple cheat sheet dealing with op-amp circuits. fundamentals and explanation
create simple cheat sheet dealing with op-amp circuits. fundamentals and explanation
Solutions
Expert Solution
| Configurations | Characteristics | |
|---|---|---|
| Comparator |  |
Compares two voltages and switches its output to indicate which
voltage is larger.
(where |
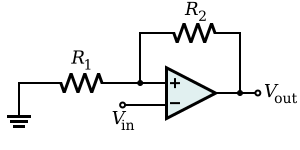
| Inverting amplifier |  |
An inverting amplifier uses negative feedback to invert and
amplify a voltage. The Rf resistor allows some of the
output signal to be returned to the input. Since the output is 180°
out of phase, this amount is effectively subtracted from the input,
thereby reducing the input into the operational amplifier. This
increases the overall gain of the amplifier and is dubbed negative
feedback.[1]
The gain of the amplifier is determined by the ratio of Rf to Rin. That is:
|
| Non-inverting amplifier |  |
Amplifies a voltage (multiplies by a constant greater than 1)
|
| Differential amplifier |  |
The circuit shown is used for finding the difference of two
voltages each multiplied by some constant (determined by the
resistors).
The name "differential amplifier" should not be confused with the "differentiator", also shown on this page.
For common-mode rejection, anything done to one input must be done to the other. The addition of a compensation capacitor in parallel with Rf, for instance, must be balanced by an equivalent capacitor in parallel with Rg. The "instrumentation amplifier" is another form of differential amplifier that also provides high input impedance. Whenever
When
|
| Voltage follower |  |
Used as a buffer amplifier to eliminate loading effects (e.g.,
connecting a device with a high source impedance to a device with a
low input impedance).
Due to the strong (i.e., unity gain) feedback and certain non-ideal characteristics of real operational amplifiers, this feedback system is prone to have poor stability margins. Consequently, the system may be unstable when connected to sufficiently capacitive loads. In these cases, a lag compensation network (e.g., connecting the load to the voltage follower through a resistor) can be used to restore stability. The manufacturer data sheet for the operational amplifier may provide guidance for the selection of components in external compensation networks. Alternatively, another operational amplifier can be chosen that has more appropriate internal compensation. |
| Summing amplifier |
|
A summing amplifer sums several (weighted) voltages:
|
| Inverting integrator | 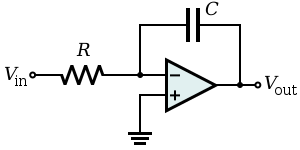 |
Integrates the (inverted) signal over time
(where
|
| Inverting differentiator |  |
Differentiates the (inverted) signal over time.
|
| Instrumentation amplifier | 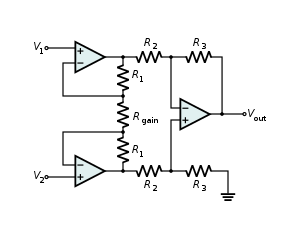 |
Combines very high input impedance, high common-mode rejection,
low DC offset, and other properties used in making very accurate,
low-noise measurements
|
| Schmitt trigger | A bistable multivibrator implemented as a comparator with
hysteresis. |
In this configuration, the input voltage is applied through the
resistor (which may be the source internal resistance) to the non-inverting
input and the inverting input is grounded or referenced. The
hysteresis curve is non-inverting and the switching thresholds are
(which may be the source internal resistance) to the non-inverting
input and the inverting input is grounded or referenced. The
hysteresis curve is non-inverting and the switching thresholds are
 where
where  is the greatest output magnitude of the operational amplifier.
is the greatest output magnitude of the operational amplifier.
Alternatively, the input source and the ground may be swapped.
Now the input voltage is applied directly to the inverting input
and the non-inverting input is grounded or referenced. The
hysteresis curve is inverting and the switching thresholds are
|
| Relaxation oscillator | 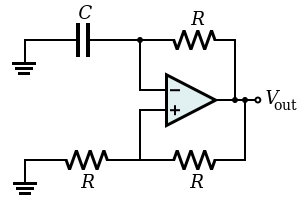 |
By using an RC network to add slow negative feedback to the inverting Schmitt trigger, a relaxation oscillator is formed. The feedback through the RC network causes the Schmitt trigger output to oscillate in an endless symmetric square wave (i.e., the Schmitt trigger in this configuration is an astable multivibrator). |
| Inductance gyrator |  |
Simulates an inductor (i.e., provides inductance without the
use of a possibly costly inductor). The circuit exploits the fact
that the current flowing through a capacitor behaves through time
as the voltage across an inductor. The capacitor used in this
circuit is smaller than the inductor it simulates and its
capacitance is less subject to changes in value due to
environmental changes.
This circuit is unsuitable for applications relying on the back EMF property of an inductor as this will be limited in a gyrator circuit to the voltage supplies of the op-amp. |
| Voltage divider reference |
|
|
| Negative impedance converter (NIC) |  |
Creates a resistor having a negative value for any signal generator
In general, the components |
| Wien bridge oscillator |  |
Produces a very low distortion sine wave. Uses negative temperature compensation in the form of a light bulb or diode. |
| Precision rectifier |  |
The voltage drop VF across the forward biased diode
in the circuit of a passive rectifier is undesired. In this active
version, the problem is solved by connecting the diode in the
negative feedback loop. The op-amp compares the output voltage
across the load with the input voltage and increases its own output
voltage with the value of VF. As a result, the voltage
drop VF is compensated and the circuit behaves very
nearly as an ideal (super) diode with VF = 0 V.
The circuit has speed limitations at high frequency because of the slow negative feedback and due to the low slew rate of many non-ideal op-amps. |
| Logarithmic output |  |
* The relationship between the input voltage and the output voltage
and the output voltage
where
where
This, when the voltage is greater than zero, can be approximated by:
Putting these two formulae together and considering that the
output voltage is the negative of the voltage across the diode
Note that this implementation does not consider temperature stability and other non-ideal effects. |
| Exponential output |  |
* The relationship between the input voltage and the output voltage
and the output voltage  is given by:
is given by:
where
when the voltage is greater than zero, it can be approximated by:
The output voltage is given by:
|
Related Solutions
Create an Op AMP based circuit that converts a 2 Vpp 350 Hz Square wave (Vin)...
Create a noninverting schmitt trigger using voltage divider as it reference voltage. Designt requirement: 1. Op-amp(comparator)...
- 1. you want to buy your dream car which will cost you $5900. If you could...
- Determine the mass (in g) of Ca3(PO4)2 that is produced when 140 mL of a 8.48×10-2...
- Scenario 2: Mrs Fei Hong (Questions 8-13 refer to this scenario) On Sunday at 1000hrs, you...
- A tank contains a two-phase liquid–vapor mixture of Refrigerant 22 at 10 bar. The mass of...
- A sinusoidal voltage Δv = 42.5 sin(100t), where Δv is in volts and t is in...
- Kelly, a 45-year old female patient, is undergoing a breast biopsy. The surgeon has just injected...
- C Programming The score table will be printed by reading the match information made between the...

 is the supply voltage and the opamp is powered by
is the supply voltage and the opamp is powered by and
and  .)
.)
 (because
(because  is a virtual ground)
is a virtual ground) , added between the non-inverting input and ground, while not
necessary, minimizes errors due to input bias
currents.[2]
, added between the non-inverting input and ground, while not
necessary, minimizes errors due to input bias
currents.[2]


 in parallel with
in parallel with 

 source and the non-invertinginput will ensure the impedances
looking out of each input will be matched.
source and the non-invertinginput will ensure the impedances
looking out of each input will be matched.
 (between the two input pins) =
(between the two input pins) = (Note: this is approximate)
(Note: this is approximate) and
and ,
the differential gain is
,
the differential gain is and
and 
 and
and  the differential gain is A = 1 and the circuit acts as a
differential follower:
the differential gain is A = 1 and the circuit acts as a
differential follower:

 (realistically, the differential input impedance of the op-amp
itself, 1 MΩ to 1 TΩ)
(realistically, the differential input impedance of the op-amp
itself, 1 MΩ to 1 TΩ)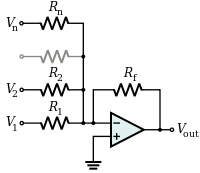

 , and
, and  independent
independent




 are functions of time,
are functions of time,  is the output voltage of the integrator at time t =
0.)
is the output voltage of the integrator at time t =
0.) ) and gain.
) and gain. can reduce the severity of this problem.
can reduce the severity of this problem.
 . Such a configuration is used in the relaxation oscillator shown
below.
. Such a configuration is used in the relaxation oscillator shown
below.
 need not be resistors; they can be any component that can be
described with an impedance.
need not be resistors; they can be any component that can be
described with an impedance.
 is the saturation current and
is the saturation current and  is the thermal voltage.
is the thermal voltage.
 is the current through the diode. As known, the relationship
between the current and the voltage for a diode is:
is the current through the diode. As known, the relationship
between the current and the voltage for a diode is:

 ), the relationship is proven.
), the relationship is proven.


 Manojponduru answered 2 years ago
Manojponduru answered 2 years ago