Question
In: Economics
2. One of the leading treadmill manufacturers has estimated the following demand equation using data from...
2. One of the leading treadmill manufacturers has estimated the following demand equation using data from 66 stores around the country: Q =+ 250 – 4P + 20A + 3Pc - 15Ac + 40 I (1.8) (20) (1.2) (18) (15) R2 = 0.78 F = 30.86 The variables and their assumed values are Q = Quantity P = Price of basic model = $1000 A =Advertising expenditures = 60 units (in thousands) =Average price of the competitor’s product = $1200 = competitor’s advertising expenditures = 70 units (in thousands) I = per capita income = 75 units (in thousands) a. Compute the elasticities for each variable. On this basis, discuss the relative impact that each variable has on the demand. What implications do these results have for the firm’s marketing, pricing, and production policies? b. What would be the effect of a 6 unit increase in the competitor’s advertising expenditures on Q? What would be the change in your advertising expenditures to offset your competitor’s strategy? c. Conduct a t-test for the statistical significance of each variable. Discuss the results of the t-tests in light of the policy implications mentioned. d. What proportion of the variation in sales is explained by the independent variables in the equation? How confident are you about this answer? Explain
Solutions
Expert Solution
2. The regression is given to be  . For the given values, the quantity would be as
. For the given values, the quantity would be as  or
or  units.
units.
(a) The elasticities would be as below.
 or
or  or
or  or
or  or
or  .
.
 or
or  or
or  or
or  or
or  .
.
 or
or  or
or  or
or  or
or  .
.
 or
or  or
or  or
or  or
or  .
.
 or
or  or
or  or
or  or
or  .
.
As can be seen, the impact is
- For a unit percent increase in price, the quantity is decreased by 1.33%.
- For a unit percent increase in advertisement, the quantity is increased by 0.4%.
- For a unit percent increase in price of competitive product, the quantity is increased by 1.2%.
- For a unit percent increase in advertisement of competitive product, the quantity is decreased by 0.35%.
- For a unit percent increase in income, the quantity is increased by 1%.
The demand is hence elastic with respect to own price and price of competitive product, and the demand is inelastic with respect to advertisement of their own and their competitive product. The demand is unitary elastic to income. The impact on demand is hence more by their own price and price of competitive product, while advertisement of their own and competitive product impacts the demand less. The impact of increase in income in this case is neither more nor less.
Thus, for the firm in question, pricing is more important than marketing, and production policies should consider more on competitive price and less on competitive advertisement, being indifferent (neither more nor less emphasize) towards income.
(b) The slope coefficient of competitive advertisement is -15, meaning that for a unit increase in competitive advertisement, the quantity decreases by 15 units. Hence, for increase in it by 6 units, the demand would decrease by 15*6=90 units.
To match for this, the own advertisement expenditure would have to be increased by 90/20=4.5 units, since for a unit increase in own advertisement, the demand increases by 20 units.
(c) The t-test would have the null hypothesis
as  and alternate hypothesis as
and alternate hypothesis as  , for i=P,A,Pc,Ac,I.
, for i=P,A,Pc,Ac,I.
Note: The number of parameters to estimate is k=6, including
intercept. From the relation between F and R-square, we have
 or
or  or
or  or
or  or
or  or
or  , suggesting that there must be 50 observations.
, suggesting that there must be 50 observations.
The 5 percent critical t would be  .
.
The test-statistics and test would be as below.
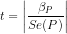 or
or 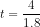 or
or 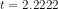 . Since
. Since 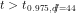 , we may reject the null, and state that the variable P is
significant.
, we may reject the null, and state that the variable P is
significant.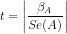 or
or 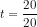 or
or 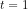 . Since
. Since 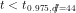 , we fail to reject the null, and state that the variable A is not
significant.
, we fail to reject the null, and state that the variable A is not
significant.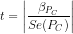 or
or 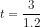 or
or 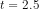 . Since
. Since 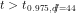 , we may reject the null, and state that the variable Pc is
significant.
, we may reject the null, and state that the variable Pc is
significant.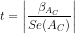 or
or 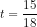 or
or 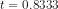 . Since
. Since 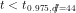 , we fail to reject the null, and state that the variable Ac is
not significant.
, we fail to reject the null, and state that the variable Ac is
not significant.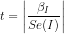 or
or 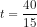 or
or 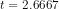 . Since
. Since 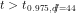 , we may reject the null, and state that the variable I is
significant.
, we may reject the null, and state that the variable I is
significant.
This confirms that the advertisement and competitive advertisement should be less emphasized as their coefficients are not significant, while price and competitive prices should be more emphasized as their coefficients are significant. Now, the income variable is significant, and yet having unit elasticity, should be emphasized more.
(d) The R-square of 0.78 suggests that 78% of
the variation in Q is explained by variations in the independent
variable. The F-statistic of F=30.89, which is greater than
 , suggests that the R-squared is significant as it passes the test
of overall significance (ie. at least one variable is
significant).
, suggests that the R-squared is significant as it passes the test
of overall significance (ie. at least one variable is
significant).
Related Solutions
2. One of the leading refrigerator producers has estimated the following demand equation after analyzing 36...
One of the leading washer and dryer manufactures has estimated the following demand equation based on...
One of the leading television providers has estimated the following demand equation after analyzing 36 regional...
The maker of a leading brand of low-calorie microwavable food estimated the following demand equation for...
The maker of a leading brand of low-calorie microwavable food estimated the following demand equation for...
Given the following estimated demand equation Answer the following questions “From the data for 50 States...
Given the following estimated demand equation Answer the following questions “From the data for 50 States...
Using the data on 4137 college students, the following equation was estimated Using the data on...
3.The marker of a leading brand of low-calorie microwavable food estimated the following demand equation for...
Company has grown from a local electronics retail store to one of leading manufacturers and distributor...
- If you take a two-litre plastic soda bottle and blow across the lid, you get a...
- A positron with kinetic energy 2.5 keV is projected into a uniform magnetic field Bvec of...
- examples of where a country/Today/ has an Absolute Advantage, and why there is an increase in...
- Suppose the charge q2 in the figure can be moved left or right along the line...
- define the following functional plans MBO mission
- I am new to python, and i used python 3. i have to make a new...
- The December 31, 20X8, balance sheets for Pint Corporation and its 70 percent-owned subsidiary Saloon Company...
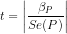 or
or 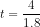 or
or 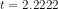 . Since
. Since 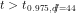 , we may reject the null, and state that the variable P is
significant.
, we may reject the null, and state that the variable P is
significant.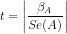 or
or 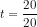 or
or 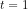 . Since
. Since 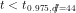 , we fail to reject the null, and state that the variable A is not
significant.
, we fail to reject the null, and state that the variable A is not
significant.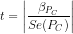 or
or 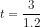 or
or 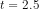 . Since
. Since 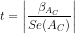 or
or 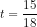 or
or 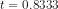 . Since
. Since 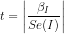 or
or 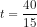 or
or 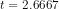 . Since
. Since  Rahul Sunny answered 2 years ago
Rahul Sunny answered 2 years ago