Question

A hydraulic press for compacting powdered samples has a large cylinder which is 10.0 cm in diameter, and a small cylinder with a diameter of 2.0 cm. A lever is attached to the small cylinder as shown in (Figure 1). The sample, which is placed on the large cylinder, has an area of 4.0 cm2.

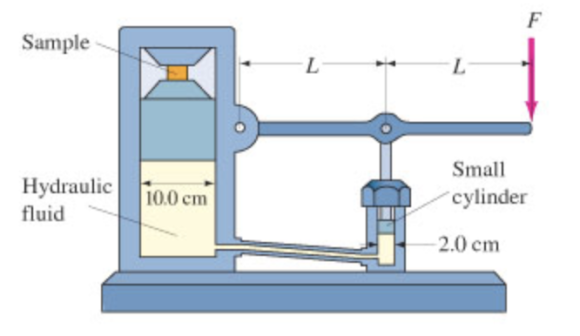
What is the pressure on the sample if F = 320N is applied to the lever?

Express your answer to two significant figures and include the appropriate units.

Answer 1

Concepts and reason

The concept of rotational equilibrium, pressure, and force is required to answer the problem First, use the condition of rotational equilibrium and determine the force acting on the small cylinder. Then, determine the pressure acting on the small cylinder using the relation between pressure, force, and area. After that, determine the force acting on the large cylinder using the relation between pressure, force, and area. Finally, determine the pressure acting on the sample using the value of the force acting on the large cylinder.

Fundamentals

Torque about a point is equal to the product of applied force and the perpendicular distance from the axis of rotation to the line of force. The expression for torque is, \(\tau=F r_{\perp}\)

Here, \(\mathrm{F}\) is the force and \(r_{\perp}\) is the perpendicular distance from the axis of rotation to the line of force. An object is said to be in rotational equilibrium when the sum of all the external torques acting on the object is zero. \(\Sigma \tau=0\)

The pressure on an object is equal to the force acting on the object divided by the area of contact. It can be expressed as, \(P=\frac{F}{A}\)

Here, \(\mathrm{P}\) is the pressure on the object, \(\mathrm{F}\) is the force on the object, and \(\mathrm{A}\) is the area of the surface on which the pressure is applied.

 

The following figure is showing the forces acting on the system. Here, \(F_{\mathrm{N}}\) is the force applied by the small cylinder.

Refer the above figure, and determine the net torque about the pivot point P. Take the anticlockwise direction of rotation as positive torque and clockwise direction as negative torque. 

\(\Sigma \tau=F_{N} L-F(2 L)\)

The net torque about the point \(\mathrm{P}\) is zero. \(\Sigma \tau=0\)

Substitute 0 for \(\Sigma \tau\) in equation \(\Sigma \tau=F_{N} L-F(2 L)\) and solve for \(F_{\mathrm{N}}\)

\(0=F_{N} L-F(2 L)\)

\(F_{N} L=F(2 L)\)

\(F_{N}=2 F\)

 

The pressure on the fluid in the small cylinder is, \(P=\frac{F_{N}}{A_{\text {small }}}\)

Here, \(A_{\text {small }}\) is the cross-sectional area of the small cylinder. Substitute \(\pi\left(\frac{d}{2}\right)^{2}\) for \(A_{\text {small }}\) and \(2 \mathrm{~F}\) for \(F_{\mathrm{N}}\) in the above equation.

$$ P=\frac{2 F}{\pi\left(\frac{d}{2}\right)^{2}} $$

\(=\frac{8 F}{\pi d^{2}}\)

Here, \(\mathrm{d}\) is the diameter of the small cylinder. Substitute \(320 \mathrm{~N}\) for \(\mathrm{F}\) and \(2.0 \mathrm{~cm}\) for \(\mathrm{d}\) in the above equation and determine the pressure acting on the small cylinder.

$$ \begin{aligned} P &=\frac{8(320 \mathrm{~N})}{\pi\left(2.0 \mathrm{~cm}\left(\frac{10^{-2} \mathrm{~m}}{1 \mathrm{~cm}}\right)\right)^{2}} \\ &=2.037 \times 10^{6} \mathrm{~Pa} \end{aligned} $$

Torque about a point is equal to the product of the force and the perpendicular distance from the axis of rotation to the line of force. The perpendicular distance from point \(C\) to the line of force \(F\) is \(2 \mathrm{~L} .\) Hence, the torque due to the force \(\mathrm{F}\) is \(F(2 L)\). Similarly, the perpendicular distance from point \(\mathrm{C}\) to the line of force \(F_{\mathrm{N}}\) is \(\mathrm{L}\). Therefore, the torque due to the force \(F_{\mathrm{N}}\) is \(F_{\mathrm{N}} L\).

 

Pressure acting on fluid can also be expressed as, \(P=\frac{F_{\text {large }}}{A_{\text {large }}}\)

Here, \(F_{\text {large }}\) is the force acting on the large cylinder and \(A_{\text {large }}\) is the area of the large cylinder. Substitute \(\pi\left(\frac{D}{2}\right)^{2}\) for \(A_{\text {large }}\) and rearrange the above equation for \(F_{\text {large }}\)

$$ P=\frac{F_{\text {large }}}{\pi\left(\frac{D}{2}\right)^{2}} $$

\(F_{\text {large }}=\frac{\pi D^{2} P}{4}\)

Substitute \(2.037 \times 10^{6} \mathrm{~Pa}\) for \(\mathrm{P}\) and \(10.0 \mathrm{~cm}\) for \(\mathrm{D}\) in the above equation and determine the force acting on the large cylinder.

$$ \begin{array}{c} F_{\text {large }}=\frac{\pi(10.0 \mathrm{~cm}(100 \mathrm{~cm}))^{2}\left(2.037 \times 10^{6} \mathrm{~Pa}\right)}{4} \\ =1.56 \times 10^{4} \mathrm{~N} \end{array} $$

The force acting on the sample is same as the force on the large cylinder. Thus, the pressure on the sample is given

as, \(P_{\mathrm{s}}=\frac{F_{\text {large }}}{A_{\mathrm{s}}}\)

Here, \(A_{\mathrm{s}}\) is the cross-sectional area of the sample. Substitute \(1.56 \times 10^{4} \mathrm{~N}\) for \(F_{\text {large }}\) and \(4.0 \mathrm{~cm}^{2}\) for \(A_{\mathrm{s}}\) in the above equation and determine the pressure on the sample.

$$ \begin{aligned} P_{\mathrm{s}} &=\frac{1.56 \times 10^{4} \mathrm{~N}}{4.0 \mathrm{~cm}^{2}\left(\frac{10^{-4} \mathrm{~m}^{2}}{1 \mathrm{~cm}^{2}}\right)} \\ &=4.0 \times 10^{7} \mathrm{~Pa} \end{aligned} $$

The pressure on the sample is \(4.0 \times 10^{7} \mathrm{~Pa}\).

The fluid in the small and large cylinder is same. Thus, the pressure on the fluid in the small cylinder is same as the pressure on the fluid in the large cylinder. Also, the force applied by the force on the large cylinder is same as the force on the small sample.

The pressure on the sample is \(4.0 \times 10^{7} \mathrm{~Pa}\).