Question

The phase diagram of Iron – Carbon:

Consider a 94 wt% Fe – 6 wt% C steel

at a temperature just below the eutectic point

shown in the Figure 9.24

for this problem.

(a)

Determine the compositions of cementite and austenite.

(b)

Determine the amount of cementite (in grams) that forms in 200g of steel.

(c)

Determine the amount of lamellar structure and pro-eutectic austenite in the 200g.

Answer 1

Concepts and reason

Phase diagram:

It is also referred to as an equilibrium diagram or constitutional diagram that displays the phase structure of an alloy at various temperatures during either heating or cooling. The steel alloys in the simplest form are mainly composed of Iron and carbon. The property of the alloyed steel depends on the percentage of carbon added to the iron at different temperatures. The iron-carbon phase diagram shows the formation of various compounds on the addition of different percentages of carbon in Iron. The concept used to solve this problem is Iron-Carbon phase diagram. Use the concept of Iron carbon phase diagram to calculate the composition of cementite and austenite. Use the concept of basic weight calculation using the iron-carbon phase diagram to calculate the amount of cementite and austenite.

Fundamentals

The formula to calculate the mass fraction of solid-phase \(\left(W_{\alpha}\right)\) is as follows:

\(W_{\alpha}=\frac{C_{L}-C_{0}}{C L-C \alpha}\)

Here, concentration of liquid phase is \(C_{L},\) initial composition of alloy is \(C_{0}\) and concentration of solid phase is \(C_{\alpha}\) The formula to calculate the mass fraction of liquid phase \(\left(W_{L}\right)\) is as follows:

\(W_{L}=\frac{C_{0}-C_{\alpha}}{C L-C \alpha}\)

 

(a)

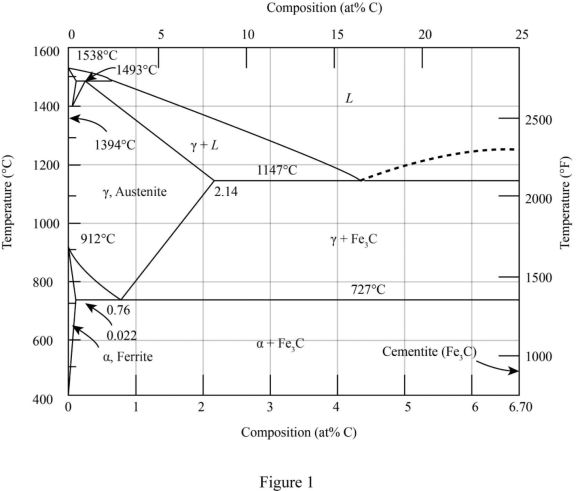
Draw the schematic representation of the Iron-Carbon phase diagram as shown in Figure (1).

Write the steps to calculate the composition of Cementite and Austenite from the Iron-Carbon phase diagram.

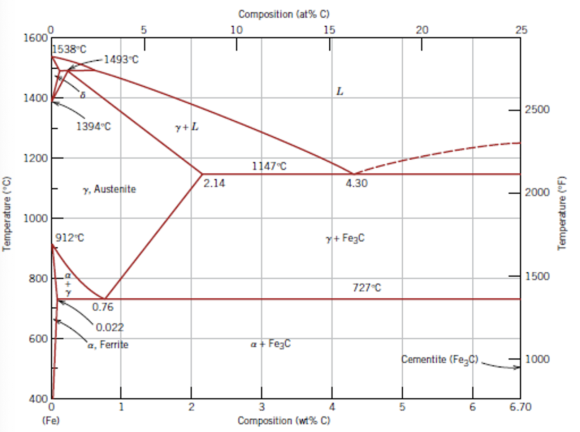
1. Locate the points up to which the regions of austenite and cementite exist.

2. Obtain the corresponding points on the x-axis from the points up to which the regions of austenite and cementite exist. From Figure-(1), construct a tie line from the temperature point to the nearest phase boundary. Draw a vertical line from the intersection point of the tie line with the solidus line to find the composition of austenite. The composition of austenite is calculated as \(2.14 \mathrm{wt} \%\) and the composition of cementite is calculated as \(6.67 \mathrm{wt} \%\)

Part a The composition of cementite is \(6.67 \mathrm{wt} \%\) and the composition of austenite is \(2.14 \mathrm{wt} \%\)

The composition of cementite and austenite is calculated with the help of Iron-Carbon phase diagram by locating the composition points on the phase diagram.

 

(b)

Write the formula to calculate the amount of cementite \(\left(\mathrm{W}_{\text {cementite}}\right)\) that forms steel. \(\mathrm{W}_{\text {cementite}}=\frac{C_{o}-C_{\gamma}}{C \mathrm{Fe}_{3} \mathrm{C}-\mathrm{C}_{\gamma}} \times \mathrm{W}_{\text {steel}}\)

Here, the carbon percentage of steel is \(C_{o}\), carbon percentage of cementite is \(C_{\mathrm{Fe} 3 \mathrm{C}}\), carbon percentage in austenite is \(C_{\gamma}\) and the weight of the steel is \(\mathrm{W}_{\text {steel}}\). Substitute \(6 \mathrm{wt} \%\) for \(C_{o}, 2.14 \mathrm{wt} \%\) for \(C_{\gamma}, 6.7 \mathrm{wt} \%\) for \(C_{\mathrm{Fe} 3 \mathrm{C}}\) and \(200 \mathrm{~g}\) for \(\mathrm{W}_{\text {steel}}\)

$$ \begin{aligned} \mathrm{W}_{\text {cementite}}=& \frac{6 \mathrm{w} \%-2.14 \mathrm{w} \mathrm{t} \%}{6.7 \mathrm{wt} \%-2.14 \mathrm{wt} \%} \times 200 \mathrm{~g} \\ =& 0.846 \times 200 \mathrm{~g} \\ &=169.2 \mathrm{~g} \end{aligned} $$

Part b The amount of cementite that forms \(200 \mathrm{~g}\) of steel is \(169.2 \mathrm{~g}\).

The amount of cementite is obtained by taking the ratio of difference of carbon content of steel and austenite and the difference of carbon content of cementite and austenite and then multiplying this ratio with the amount of steel to be formed.

 

(c)

Write the formula to calculate the amount of lamellar structure (W \(_{\text {lamellar}}\) ) \(\mathrm{W}_{\text {lamellar}}=\frac{C_{o}-C \gamma}{\text {Clamellar}-\mathrm{C}_{\gamma}} \times \mathrm{W}_{\text {steel}}\)

Obtain the carbon content to form austenite for a lamellar structure as \(0.76 \mathrm{wt} \%\) using Figure (1). Substitute \(6 \mathrm{wt} \%\) for \(C_{o}, 0.76 \mathrm{wt} \%\) for \(C_{\gamma}, 6.7 \mathrm{wt} \%\) for \(C_{\text {lamellar}}\) and \(200 \mathrm{~g}\) for \(\mathrm{W}_{\text {steel}}\)

$$ \begin{aligned} \mathrm{W}_{\text {lamellar}}=& \frac{6 \mathrm{wt} \%-0.76 \mathrm{wt} \%}{6.7 \mathrm{wt} \%-0.76 \mathrm{wt} \%} \times 200 \mathrm{~g} \\ =& 0.882 \times 200 \mathrm{~g} \\ &=176.43 \mathrm{~g} \end{aligned} $$

Write the equation to calculate the amount of pro eutectic austenite \(\left(\mathrm{W}_{\gamma}\right)\). \(\mathrm{W}_{\gamma}=\mathrm{W}_{\text {steel}}-\mathrm{W}_{\text {lamellar}}\)

Substitute \(200 \mathrm{~g}\) for \(\mathrm{W}_{\text {steel}}\) and \(176.43 \mathrm{~g}\) for \(\mathrm{W}_{\text {lamellar}}\)

$$ \begin{aligned} \mathrm{W}_{\gamma}=& 200 \mathrm{~g}-176.43 \mathrm{~g} \\ &=23.57 \mathrm{~g} \end{aligned} $$

Part c The amount of lamellar structure is \(176.43 \mathrm{~g}\) and the amount of pro eutectic austenite is \(23.57 \mathrm{~g}\).

The amount of lamellar structure is obtained by taking the ratio of difference of carbon content of steel and austenite and the difference of carbon content of lamellar structure and austenite and then multiplying this ratio with the amount of steel.