Question

Create a graph of y=2x−6.

Construct a graph corresponding to the linear equation y=2x−6.

 

Answer 1

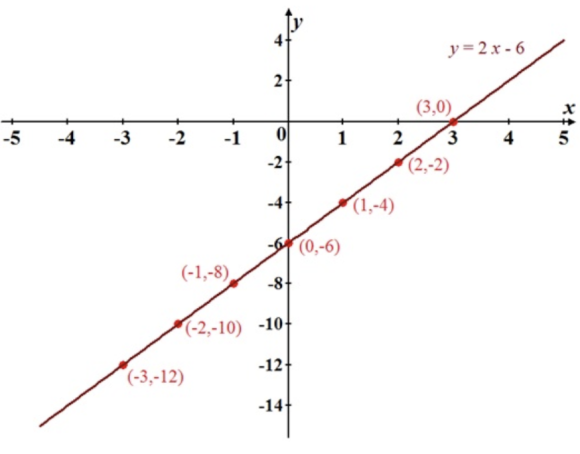
The objective is to construct a graph of the function $y=2 x-6$

In order to create a graph for the given function, take some negative and positive integer values for $x$ and determine the corresponding $y$ values. 

$$\begin{array}{|c|c|} \hline x & y=2 x-6 \\ \hline-3 & 2(-3)-6=-12 \\ -2 & 2(-2)-6=-10 \\ -1 & 2(-1)-6=-8 \\ 0 & 2(0)-6=-6 \\ 1 & 2(1)-6=-4 \\ 2 & 2(2)-6=-2 \\ 3 & 2(3)-6=0 \\ \hline \end{array}$$

From the constructed table the points on the graph are,

$$(-3,-12),(-2,-10),(-1,-8),(0,-6),(1,-4),(2,-2), \text { and }(3,0)$$

Plot the points on Co-ordinate axes and join them with smooth curve.