Question

In the figure(Figure 1), a proton is fired with a speed of 200,000m/s from the midpoint of the capacitor toward the positive plate.

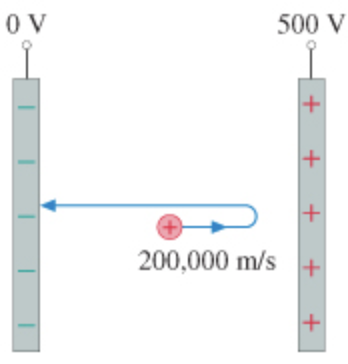
What is the proton's speed as it collides with the negative plate?

Answer 1

Concepts and reason

The concepts used to solve this problem are parallel plate capacitor, potential inside the parallel plate capacitor, speed and conservation of energy. Using law of conservation of energy, find the speed of the proton as it collides with the negative plate.

Fundamentals

The expression for the initial kinetic energy of the proton is, \(K_{i}=\frac{1}{2} m v_{i}^{2}\)

Here, \(K_{i}\) is the initial kinetic energy, \(\mathrm{m}\) is the mass of proton, and \(v_{i}\) is initial speed of the proton. The expression for the final kinetic energy of the proton is, \(K_{f}=\frac{1}{2} m v_{f}^{2}\)

Here, \(K_{f}\) is the final kinetic energy, \(\mathrm{m}\) is the mass of proton, and \(v_{f}\) is final speed of the proton. The expression for the initial potential energy of the proton is, \(U_{i}=q V_{i}\)

Here, \(U_{i}\) is the initial potential energy, \(\mathrm{q}\) is the charge of proton, and \(V_{i}\) is the initial potential of the proton. The expression for the final potential energy of the proton is, \(U_{f}=q V_{f}\)

Here, \(U_{f}\) is the final potential energy and \(V_{f}\) is the final potential of the proton. From the law of conservation of energy the expression is, \(E_{i}=E_{f}\)

Here, \(E_{i}\) is the total initial energy and \(E_{f}\) is the total final energy of the proton.

 

Expression for the initial kinetic energy of the proton is, \(K_{i}=\frac{1}{2} m v_{i}^{2}\)

Expression for the initial potential energy of the proton is, \(U_{i}=q V_{i}\)

Expression for the total initial energy of the proton is, \(E_{i}=K_{i}+U_{i}\)

Expression for the final kinetic energy of the proton is, \(K_{f}=\frac{1}{2} m v_{f}^{2}\)

Expression for the final potential energy of the proton is, \(U_{f}=q V_{f}\)

Expression for the total initial energy of the proton is, \(E_{f}=K_{f}+U_{f}\)

From the law of conservation of energy the expression is, \(E_{i}=E_{f}\)

Substitute \(K_{i}+U_{i}\) for \(E_{i}\) and \(K_{f}+U_{f}\) for \(E_{f}\) \(K_{i}+U_{i}=K_{f}+U_{f}\)

Substitute \(\left(\frac{1}{2} m v_{i}^{2}\right)\) for \(K_{i},\left(q V_{i}\right)\) for \(U_{i},\left(\frac{1}{2} m v_{f}^{2}\right)\) for \(K_{f},\) and \(\left(q V_{f}\right)\) for \(U_{f}\) \(\frac{1}{2} m v_{i}^{2}+q V_{i}=\frac{1}{2} m v_{f}^{2}+q V_{f}\)

Explanation \(\mid\) Common mistakes \(\mid\) Hint for next step

According to law of conservation of energy in the case of isolated system, the total initial and total final energy will be equal.

 

According to law of conservation of energy the expression is, \(\frac{1}{2} m v_{i}^{2}+q V_{i}=\frac{1}{2} m v_{f}^{2}+q V_{f}\)

Rearrange the expression for \(v_{f}\)

$$ \begin{array}{c} \frac{1}{2} m v_{i}^{2}+q V_{i}=\frac{1}{2} m v_{f}^{2}+q V_{f} \\ \frac{1}{2} m v_{f}^{2}=\frac{1}{2} m v_{i}^{2}+q V_{i}-q V_{f} \\ v_{f}=\sqrt{v_{i}^{2}+\frac{2 q\left(V_{i}-V_{f}\right)}{m}} \end{array} $$

Substitute \(200,000 \mathrm{~m} / \mathrm{s}\) for \(v_{i}, 1.6 \times 10^{-19} \mathrm{C}\) for q, \(250 \mathrm{~V}\) for \(V_{i}, 0.00 \mathrm{~V}\) for \(V_{f},\) and \(1.6726 \times 10^{-27} \mathrm{~kg}\) for \(\mathrm{m}\)

$$ \begin{array}{c} v_{f}=\sqrt{(200,000 \mathrm{~m} / \mathrm{s})^{2}+\left[\frac{2\left(1.6 \times 10^{-19} \mathrm{C}\right)(250 \mathrm{~V}-0.00 \mathrm{~V})}{\left(1.6726 \times 10^{-27} \mathrm{~kg}\right)}\right]} \\ =2.96 \times 10^{5} \mathrm{~m} / \mathrm{s} \end{array} $$

The proton's speed as it collides with the negative plate is \(2.96 \times 10^{5} \mathrm{~m} / \mathrm{s}\).