Section I: Derivation of Hicksian Demand Curve Joyce’s utility function is as follows: U= 10X3Y2 Where,...

Section I: Derivation of Hicksian Demand Curve

Joyce’s utility function is as follows:

U= 10X³Y²

Where, X, is the quantity of good X consumed, Y, is the quantity of good Y consumed and, U, is Joyce’s utility function.

The general budget constraint for the two goods is a follow:

B= P_XX + P_YY

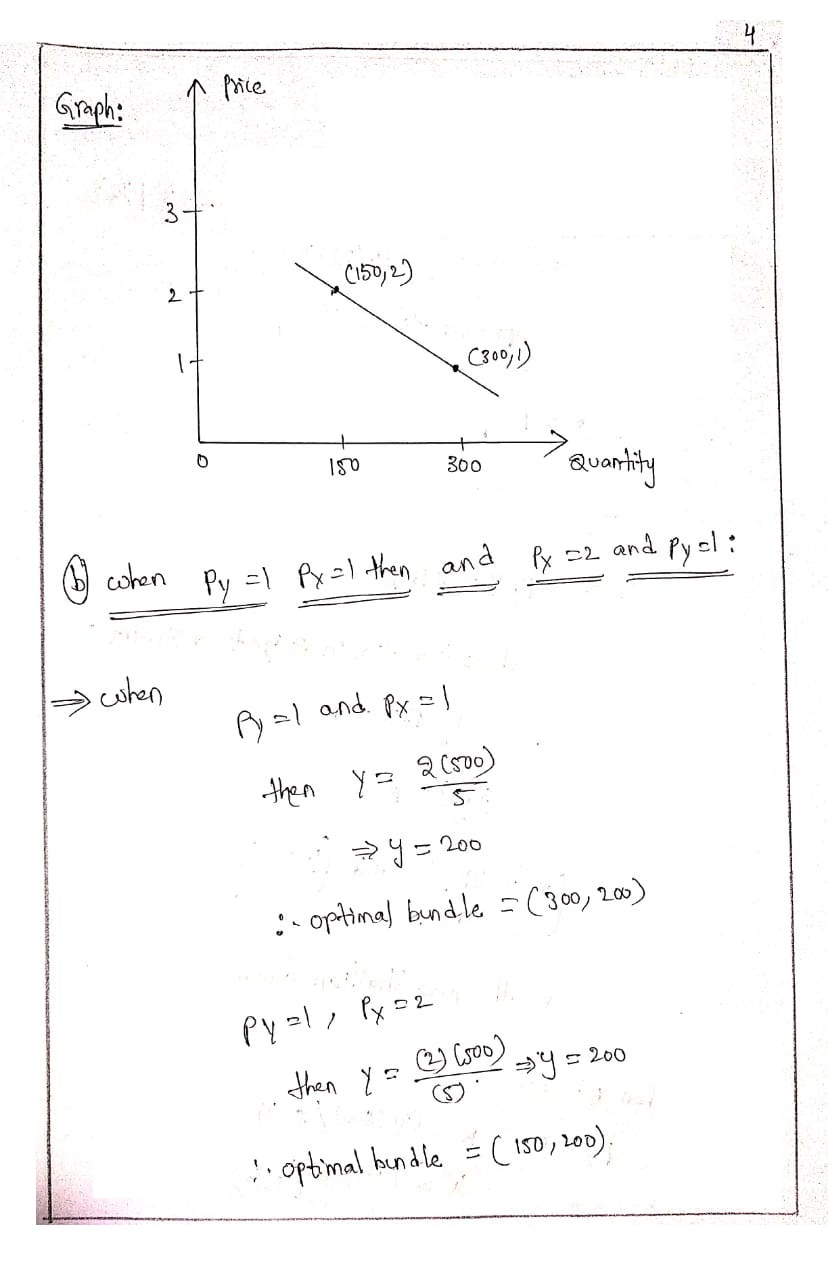
Derive Joyce’s Marshallian demand equation for good X. Also compute her demand for good X when B= 500, and the price of good X is 1 and 2. Also draw the Marshallian demand curve for X at these prices.

What is Joyce’s optimal amount of good Y purchased if P_Y= 1 and P_x=1 and if P_x=2 and P_Y= 1?

Derive the Hicksian demand for good X at these prices. Hint, you need to choose the three correct equations you’ve derived above and solve simultaneously. Also, draw both demand curves on the same graph.

Using the information derived in parts A and B, what is the substitution effect and income effect obtained when changing the price of good x from a value of 1 to a value of 2.

Expert Solution

Rahul Sunny answered 1 hour ago

Albert's utility function is U(I) = 100I2 , where Iis income.Stock I generates net-payoffs...

Albert's utility function is U(I) = 100I2 , where I is income.Stock I generates net-payoffs of $80 with probability 0.3, $100 with probability 0.4; and $120 with probability 0.3. Stock II generates net-payoffs of $80 with probability 0.1, $100 with probability 0.8; and $120 with probability 0.1.(i) Which stock should Albert select, I or II?(ii) What general point about risk-loving preferences have your illustrated?

Consider the utility function of U(X,Y) = X0.2Y0.4 Derive the Marshallian demand curve for X Derive...

Consider the utility function of U(X,Y) = X0.2Y0.4 Derive the Marshallian demand curve for X Derive the Hicksan demand curve for X What is the own-price elasticity for X? What is the income elasticity of X? What is the price elasticity of X with respect to y (Py) If the income level is 120, then what is the Pxthat maximizes total spending Show that Slutsky equation holds Show that ex,px+ex,py+ex,I=0. What does it mean? Show that Engle Aggregation holds. What does it...

Suppose that an individual has a utility function of the form U = Y½ where U...

Suppose that an individual has a utility function of the form U = Y½ where U is utility and Y is income. a) Calculate the utility level for Y values of $10,000, $40,000, $90,000, $160,000, and $250,000 and then plot the individual’s total utility function. b) This individual is currently earning $90,000 but has a 50-50 chance of earning either $40,000 or $160,000 in a new job. i) Calculate the expected income and utility from the new...

What is the relationship between the expenditure function and the Hicksian demand function?

A basic feature of the utility function (demand curve) is the law of diminishing marginal utility....

A basic feature of the utility function (demand curve) is the law of diminishing marginal utility. That is, as a person consumes an item or a product, the satisfaction or utility that they derive from the product wanes as they consume more and more of that product. In other words, the price a person is willing to pay (or the demand) for that product decreases with consumption. However, our demand for some environmental goods (e.g., clean air/water) does not wane...

16.Suppose the utility function of Nathasha was given U(I)=(ROOT10I). Where' I' represents annual income (in $1,000)....

16.Suppose the utility function of Nathasha was given U(I)=(ROOT10I). Where' I' represents annual income (in $1,000). (1)Explain whether she is risk-preferred, risk-neutral, or hedging. (2) Let's say she has a current income of $40,000 (I=40) and is sure to make the same income next year. She has a new job. New jobs have a 0.6 chance of earning $44,000 and a 0.4 chance of earning $33,000. Should she take this job? (3) In (2) will she try to insure against...

Amy’s utility function is U = √ C, where C is consumption and is given by...

Amy’s utility function is U = √ C, where C is consumption and is given by C = Income − Expenses. Amy’s income is $10,000 and there is a 5% chance that she will get sick, which would cost $3,600 in medical expenses. (a) (5 points) What is Amy’s expected utility if she doesn’t have insurance? (b) (5 points) What is the actuarially fair premium for a full-coverage insurance plan? What is the actuarially fair premium for an insurance plan...

A consumer’s utility function is U = logx + logy2 , where and y are two...

A consumer’s utility function is U = logx + logy2 , where and y are two consumption goods. The price of x is $2.00 per unit and the price of y $5.00 per unit. Her budget is $1000. Solve her utility maximization problem and find her optimal consumption of x and y. Will your answers change if the consumer’s utility function is U = logxy2 instead – why or why not?

The consumer’s utility function is U(a,b) = ab2, where a denotes the quantity of good A...

The consumer’s utility function is U(a,b) = ab2, where a denotes the quantity of good A that the consumer consumes and b denotes the quantity of good B that the consumer consumes. The price per unit of good A is 4 Euros and the price per unit of good B is 8 Euros. Consumer’s income is 120 Euros. a) Find the marginal utility of good A and the marginal utility of good B b) Find the optimal quantity of good...

Suppose that Elizabeth has a utility function U= (or U=W^(1/3) ) where W is her wealth...

Suppose that Elizabeth has a utility function U= (or U=W^(1/3) ) where W is her wealth and U is the utility that she gains from wealth. Her initial wealth is $1000 and she faces a 25% probability of illness. If the illness happens, it would cost her $875 to cure it. What is Elizabeth’s marginal utility when she is well? And when she is sick? Is she risk-averse or risk-loving? What is her expected wealth with no insurance? What is...

Question