Question

3. Suppose that a closed economy could be described by the following set of equations: Production Function: Y = 120K1/3 L2/3

̅̅ Factors of production: K=125; L=1000

̅̅ Government Behavior: G= 3000; T = 2500

Consumption Behavior: C = 400 + 0.8(Y –T)
Investment Behavior: I = 16500 – 1000r
a. Calculate the equilibrium level of output (Y)
b. Prove that the production function has the property of constant returns to scale.

c. Calculate the marginal product of labor (MPL)

d) Calculate the equilibrium levels of the following variables

(i) Consumption (C)

(ii) Private Savings

(iii) Public Savings

(iv) National Savings (S)

(v) real interest rate (r)

Answer 1

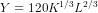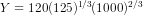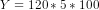3. (a) The production function is given as . For the given values of K and L, we have the equilibrium level of output as or or .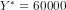

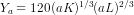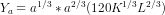(b) Increasing the input by a>1 times, we have or 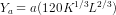or or 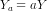. This means that increasing the input by a times would increase the output by the same a times. Hence, the production function has property of constant returns to scale.

(c) The marginal product of labor would be as

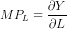
or 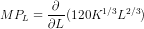(putting the production function)

or 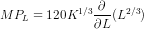(since partial differentiation with respect to L would treat the other variables as constnat)

or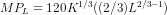

or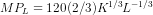

or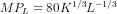

or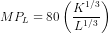

or .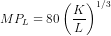

This is the amount of change in output for a marginal unit increase in the labor.

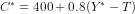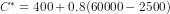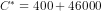(d) (i) The equilibrium consumption would be as or or or .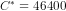

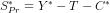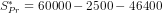(ii) The private savings would be or or .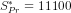

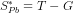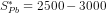(iii) The public savings would be or or .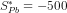

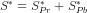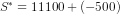(iv) The national savings would be or or 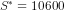. This can also be calculated by 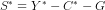, which would yield the same result.

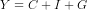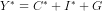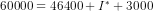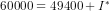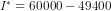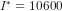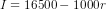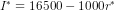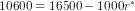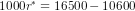(v) The national income equality is , ie or or or or (which confirms the saving income equality). Since we have investment behavior as , we have or or 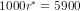or or 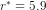(maybe percent) as the required equilibrium interest rate.