Question

In a study of the accuracy of fast food​ drive-through orders, Restaurant A had 231

accurate orders and

74

that were not accurate.a. Construct a

95​%

confidence interval estimate of the percentage of orders that are not accurate.b. Compare the results from part​ (a) to this

95​%

confidence interval for the percentage of orders that are not accurate at Restaurant​ B:

0.2160 <p<0.319

What do you​ conclude?

a. Construct a

95​%

confidence interval. Express the percentages in decimal form.

nothing less than<pless than<nothing

​(Round to three decimal places as​ needed.)

Answer 1

Solution :

Given that,

n =231

x = 74

Point estimate = sample proportion = = x / n = 74 / 231=0.320

1 - = 1 - 0.320=0.680

At 95% confidence level

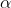= 1 - 95%

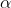=1 - 0.95 =0.05

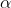/2 = 0.025

Z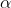/2 = Z_{0.025 = 1.96}

Margin of error = E = Z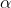 _{/ 2} * (( * (1 - )) / n)

= 1.96 (((0.320*0.680) /231 )

= 0.060

A 95% confidence interval for population proportion p is ,

0.320 - 0.060 < p < 0.320+ 0.060

0.260 < p < 0.380

(0.260 , 0.380)

The 95% confidence interval for the population proportion p is :(0.260 , 0.380)

B .0.2160 <p<0.319 is smaller than A